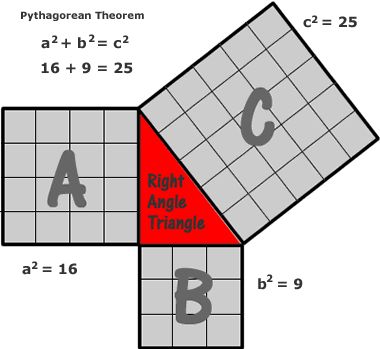
 In mathematics, the Pythagorean (Pythagoras) theorem (written around 400 BC) is a relation among the three sides of a right triangle (right-angled triangle). In terms of areas, it states:
In mathematics, the Pythagorean (Pythagoras) theorem (written around 400 BC) is a relation among the three sides of a right triangle (right-angled triangle). In terms of areas, it states:
“In any right-angled triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).”
But in reality, this was written much earlier in ancient india by sage Baudhayana (around 2000 BCE).
He is noted as the author of the earliest Sulba Sūtra—appendices to the Vedas giving rules for the construction of altars—called the Baudhāyana Śulbasûtra, which contained several important mathematical results.
He is accredited with calculating the value of pi (π) before Pythagoras.
Solka in Baudhāyana Śulbasûtra that describes Pythagoras theorem is given below :
dīrghasyākṣaṇayā rajjuH pārśvamānī, tiryaDaM mānī, cha yatpṛthagbhUte kurutastadubhayāṅ karoti.
Baudhāyana used a rope as an example in the above sloka.
Its translation means : A rope stretched along the length of the diagonal produces an area which the vertical and horizontal sides make together.
Proof of Pythagoras theorem has been provided by both Baudhāyana and Āpastamba in their Sulba Sutras.
Though, Baudhāyana was not the only Indian mathematician to have provided Pythagorean triplets and proof. Āpastamba also provided the proof for Pythagoras theorem, which is numerical in nature and unfortunately, Pythagoras was wrongly credited by Cicero and early Greek mathematicians for this theorem.
Also, another ancient Indian mathematician called Bhaskara later provided a unique geometrical proof as well as numerical which is known for the fact that it’s truly generalized and works for all sorts of triangles and is not incongruent.
